#2630_색종이 만들기 #백준 #재귀함수

https://www.acmicpc.net/problem/2630

2630번: 색종이 만들기

def divide_paper(x, y, size):

    global white, blue

    color = paper[y][x]

    for i in range(y, y + size):

        for j in range(x, x + size):

            if paper[i][j] != color:

                # 다른 색이 나오면 네 등분하여 재귀적으로 호출

                divide_paper(x, y, size // 2)

                divide_paper(x + size // 2, y, size // 2)

                divide_paper(x, y + size // 2, size // 2)

                divide_paper(x + size // 2, y + size // 2, size // 2)

                return

    # 해당 영역이 모두 같은 색이면 하얀색 또는 파란색 종이 개수 증가

    if color == 0:

        white += 1

    else:

        blue += 1

N = int(input())

paper = []

for _ in range(N):

    paper.append(list(map(int, input().split())))

white, blue = 0, 0

divide_paper(0, 0, N)

print(white)

print(blue)

#2630 code 색종이 만들기

 

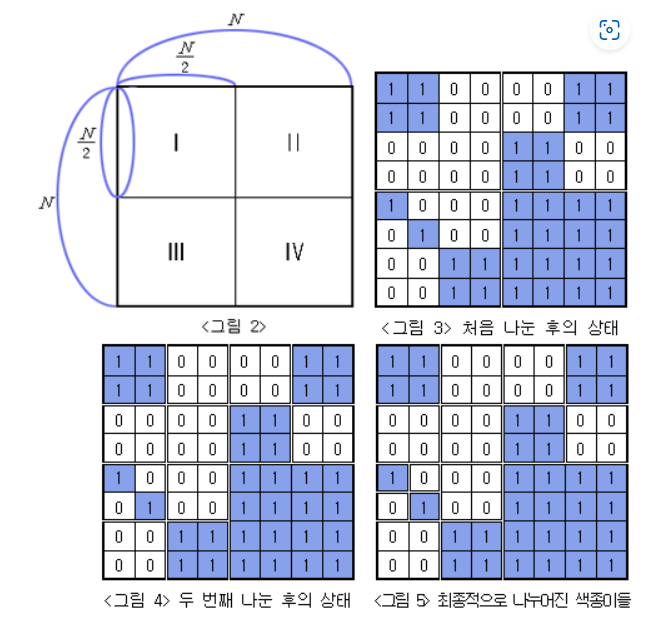
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.

위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.

 

전체 종이의 크기가 2**n으로 주어지고 전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 자랄서 <그림2>의 1,2,3,4 처럼 똑같은 크기의 네개의 n/2*n/2 부분으로 나누기 때문에 (x,y) , (x,y+n/2), (x+n/2, y), (x+n/2, y+n/2) 이 네 좌표를 시작점으로 둘 수 있다. n/2*/n/2부분으로 나누기 때문에 사이즈는 n/2 그래서 이 부분을 재귀함수로 구현을 하여 해당영역이 같은 부분이 될 때 까지 계속 재귀가 돌 수 있도록 구현을 하였다.

 

이 문제는 좀 나에게 어려워서 푸는데 1시간 반정도 걸렸다. 아직 갈길 먼 것 같다... 앞으로 더 노력을 해야겠다.